how to find an exponential function from two points

Learning Outcomes

• Given two data points, write an exponential office.
• Identify initial conditions for an exponential function.
• Find an exponential function given a graph.
• Use a graphing calculator to find an exponential part.
• Find an exponential office that models continuous growth or decay.

In the previous examples, we were given an exponential role which we then evaluated for a given input. Sometimes nosotros are given information about an exponential function without knowing the part explicitly. Nosotros must use the information to first write the class of the function, determine the constants a and b, and evaluate the function.

How To: Given ii data points, write an exponential model

1. If 1 of the data points has the form [latex]\left(0,a\right)[/latex], then a is the initial value. Using a, substitute the second betoken into the equation [latex]f\left(x\right)=a{b}^{x}[/latex], and solve for b.
2. If neither of the data points accept the course [latex]\left(0,a\right)[/latex], substitute both points into two equations with the form [latex]f\left(x\right)=a{b}^{x}[/latex]. Solve the resulting arrangement of two equations to find [latex]a[/latex] and [latex]b[/latex].
3. Using the a and b found in the steps to a higher place, write the exponential function in the form [latex]f\left(x\right)=a{b}^{x}[/latex].

Example: Writing an Exponential Model When the Initial Value Is Known

In 2006, 80 deer were introduced into a wildlife refuge. By 2012, the population had grown to 180 deer. The population was growing exponentially. Write an algebraic function N(t) representing the population Northward of deer over time t.

Try It

A wolf population is growing exponentially. In 2011, 129 wolves were counted. By 2013 the population had reached 236 wolves. What two points tin be used to derive an exponential equation modeling this situation? Write the equation representing the population N of wolves over time t.

Show Solution

[latex]\left(0,129\correct)[/latex] and [latex]\left(2,236\right);Due north\left(t\correct)=129{\left(\text{1}\text{.3526}\correct)}^{t}[/latex]

Example: Writing an Exponential Model When the Initial Value is Not Known

Detect an exponential function that passes through the points [latex]\left(-2,half dozen\right)[/latex] and [latex]\left(2,1\right)[/latex].

Try It

Given the ii points [latex]\left(one,3\correct)[/latex] and [latex]\left(two,iv.5\right)[/latex], find the equation of the exponential function that passes through these two points.

Show Solution

[latex]f\left(x\right)=2{\left(ane.5\right)}^{x}[/latex]

Q & A

Do two points always decide a unique exponential part?

Yes, provided the two points are either both above the ten-centrality or both below the x-centrality and have different 10-coordinates. But go on in heed that we also need to know that the graph is, in fact, an exponential office. Non every graph that looks exponential really is exponential. We need to know the graph is based on a model that shows the same per centum growth with each unit increase in x, which in many real world cases involves time.

How To: Given the graph of an exponential function, write its equation

1. Outset, identify two points on the graph. Choose the y-intercept as ane of the two points whenever possible. Try to choose points that are as far autonomously as possible to reduce round-off error.
2. If i of the data points is the y-intercept [latex]\left(0,a\correct)[/latex] , then a is the initial value. Using a, substitute the 2nd bespeak into the equation [latex]f\left(ten\right)=a{b}^{ten}[/latex] and solve for b.
3. If neither of the information points have the form [latex]\left(0,a\correct)[/latex], substitute both points into two equations with the form [latex]f\left(x\right)=a{b}^{x}[/latex]. Solve the resulting system of 2 equations to discover a and b.
4. Write the exponential function, [latex]f\left(x\right)=a{b}^{x}[/latex].

Example: Writing an Exponential Role Given Its Graph

Find an equation for the exponential function graphed below.

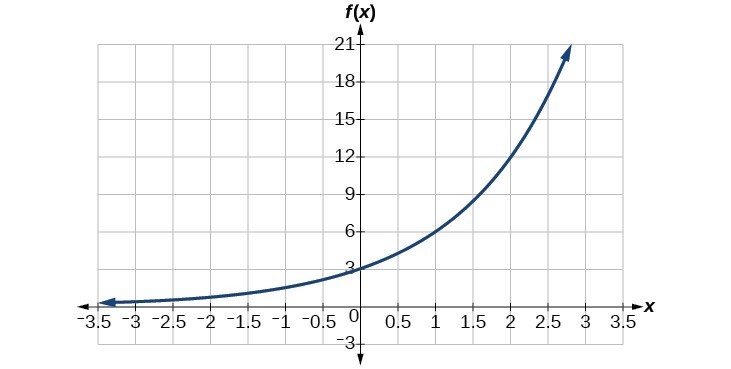
Effort It

Discover an equation for the exponential function graphed below.

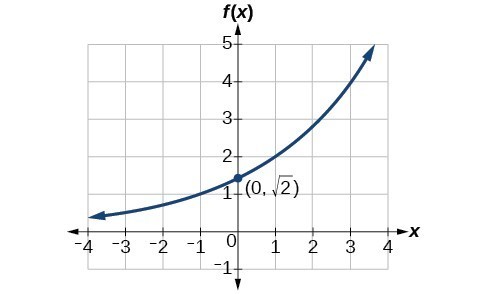
Show Solution

[latex]f\left(x\right)=\sqrt{2}{\left(\sqrt{2}\correct)}^{x}[/latex]. Answers may vary due to circular-off error. The answer should be very close to [latex]1.4142{\left(1.4142\correct)}^{x}[/latex].

Investigating Continuous Growth

So far we accept worked with rational bases for exponential functions. For most real-world phenomena, however, e is used equally the base for exponential functions. Exponential models that utilise e every bit the base of operations are called continuous growth or decay models. We see these models in finance, information science, and most of the sciences such as physics, toxicology, and fluid dynamics.

A Full general Annotation: The Continuous Growth/Decay Formula

For all real numbers t, and all positive numbers a and r, continuous growth or decay is represented past the formula

[latex]A\left(t\right)=a{e}^{rt}[/latex]

where

• a is the initial value
• r is the continuous growth rate per unit of time
• t is the elapsed time

If r> 0, then the formula represents continuous growth. If r< 0, so the formula represents continuous decay.

For business applications, the continuous growth formula is called the continuous compounding formula and takes the course

[latex]A\left(t\correct)=P{e}^{rt}[/latex]

where

• P is the principal or the initial investment
• r is the growth or interest rate per unit of time
• t is the period or term of the investment

How To: Given the initial value, charge per unit of growth or decay, and time t, solve a continuous growth or decay function

1. Use the information in the trouble to determine a, the initial value of the function.
2. Use the data in the problem to decide the growth charge per unit r.
   • If the trouble refers to continuous growth, then r> 0.
   • If the problem refers to continuous disuse, so r< 0.
3. Use the information in the problem to determine the time t.
4. Substitute the given information into the continuous growth formula and solve for A(t).

Case: Calculating Continuous Growth

A person invested $ane,000 in an account earning a nominal interest charge per unit of 10% per year compounded continuously. How much was in the business relationship at the end of one year?

Attempt It

A person invests $100,000 at a nominal 12% interest per yr compounded continuously. What will exist the value of the investment in 30 years?

Bear witness Solution

$three,659,823.44

Example: Computing Continuous Disuse

Radon-222 decays at a continuous rate of 17.3% per day. How much will 100 mg of Radon-222 disuse to in 3 days?

Try Information technology

Using the information in the previous example, how much radon-222 will remain after ane year?

Show Solution

3.77E-26 (This is estimator notation for the number written every bit [latex]3.77\times {10}^{-26}[/latex] in scientific notation. While the output of an exponential function is never zero, this number is and so close to zero that for all practical purposes we can accept zero every bit the answer.)

Contribute!

Did you have an thought for improving this content? We'd love your input.

Improve this pageLearn More

Source: https://courses.lumenlearning.com/waymakercollegealgebra/chapter/find-the-equation-of-an-exponential-function/

Posted by: barrettdetur1973.blogspot.com

Share this post